因数 分解 中 2 353786-因数分解 中2 問題

因数分解の公式の利用 Math Showme
因数分解 把一个数分解成两个或更多的除1外的整数相乘的过程。 这些整数称为这个数的因数。 如所有因数均要求为质数,则称为质因数分解。 质因数分解例如24=3*2*2*2 因数分解例如16=2*8(其一种,可分解多种)== 因数分解2 == 解説(問題は下にあります.) 次の公式を使って因数分解するときは,はじめに両端を見るのがヒケツです.真ん中は最後に見ます.
因数分解 中2 問題
因数分解 中2 問題-因数分解しなさい ①4a 2bc12ab 2c8abc 2 ②2x 25x3 ③49x 216y 2z 2 ④6x 27x3 ⑤8x 2y10xy3y ⑥x 3x ⑦x 39x 2x ⑧3ax 218ax27a ⑨ (x2) 25 (x2) ⑩ (x3) 2 (x3)12 ⑪ (2ab) 2 (a2b) 2 ⑫x 26xy9y 225 ⑬x 210x25y 2 ⑭x 22xyy 29 1の解説 2の解説因数分解を解くときの最初のコツは、 式全体を見渡して、共通する文字や数字を探す ということだよ。 x 2 +3x という式で考えてみよう。 式を見ると、「x 2 」と「3x」で、xという 文字が共通している ことがわかるよね。 こんなふうに、 共通する文字が見つかったら、それを外に出す 。

Project Euler 29 Distinct Powers 大整数质因数分解做法 普通做法 Ojnq 博客园
(考え方) 同じ式が全くないときは,単純に展開して,式を整理してから因数分解します (x1)(x4)−2(2x3)=x 2 5x4−4x−6 =x 2 x−2 積が−2となる2数は異符号(正と負).その中で和が1となるのは,正の方が強い つまり、 すべての項に2の倍数があります。 したがって、 次のように"2″を共通因数として取り出す ことができます。 2x²x42 =2(x²10x21) さらに カッコ内の"x²10x21"に注目 すると、この部分は、 x² ( )x =(x ) (x ) の公式で因数分解できますよね。 たして10になる数とかけて21になる数の組合せは、7と3なので、 2 (x²10x21) =2 (x7) (x3) これが答えになります このページでは中3の数学で押さえておきたい 「多項式の計算」「因数分解」「平方根」「二次方程式」 の基礎ポイントをご紹介させていただきます。 こんなページも見られています! >>中学3年生の教科別学習ポイント 21年4月から中学校の教科書が
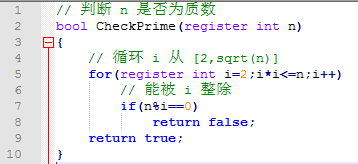
质因数分解 问题描述 求出区间a,b中所有整数的质因数分解。输入格式 输入两个整数a,b。 输出格式 每行输出一个数的分解,形如k=a1a2a3(a1 蓝桥杯 基础练习 分解质因数 C语言 描述 求出区间a,b中所有整数的质因数分解。输入 输入描述 输入两个整数a,b。 输入样例 3 10 输出 输出描述 每行输出一个数的分解,形如k=a1a2a3(a1能从上述式子中找到约数的个数6吗? 我相信你肯定会问我:是质因数2 × 3 = 6,对吗? 哈哈,刚好凑巧罢了,事实上并不对。 那会是什么呢??? 细心的你肯定是注意到了, 我在质因数2和3的右上角分别标上了它们各自的次数1和2。
因数分解 中2 問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 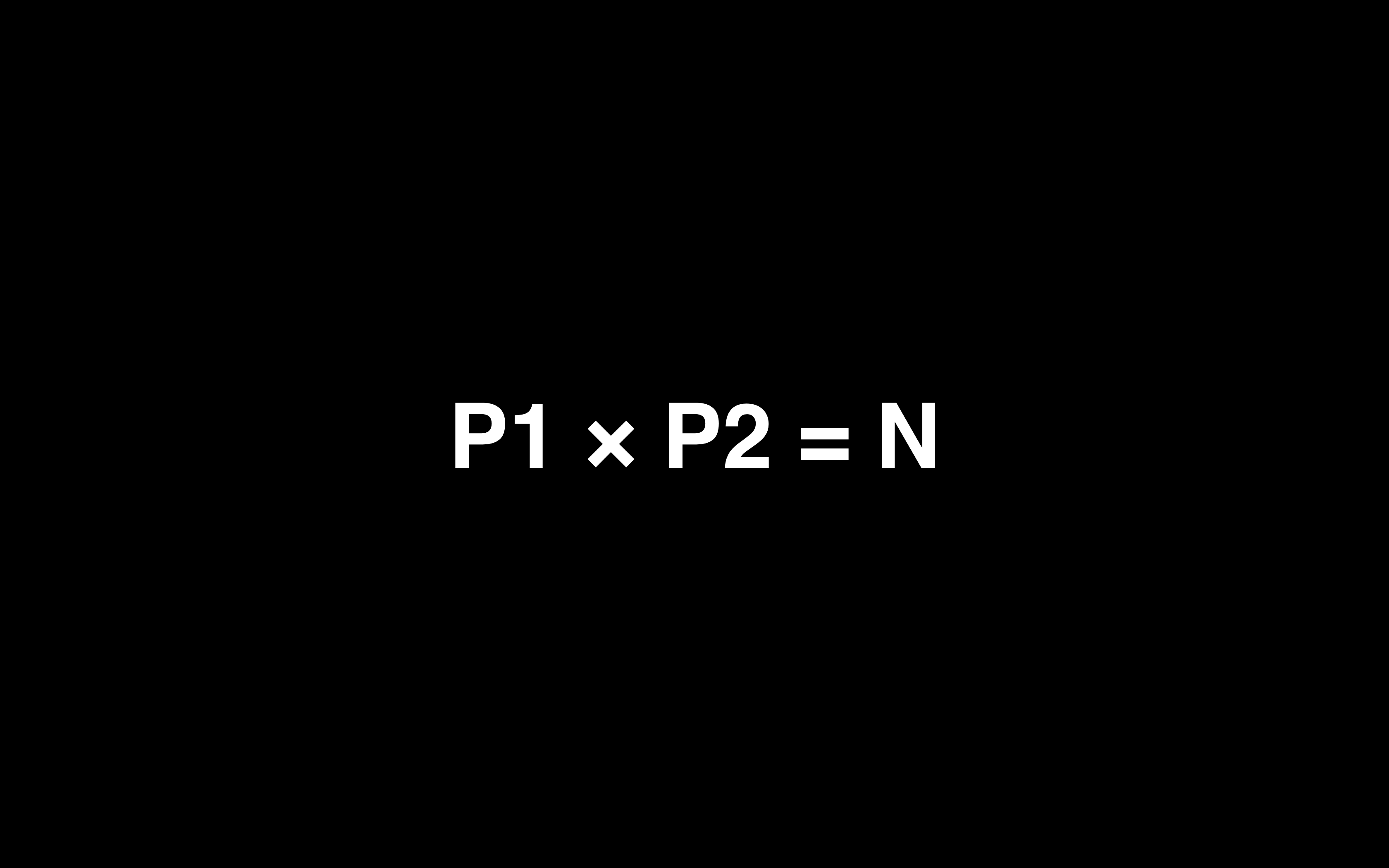 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 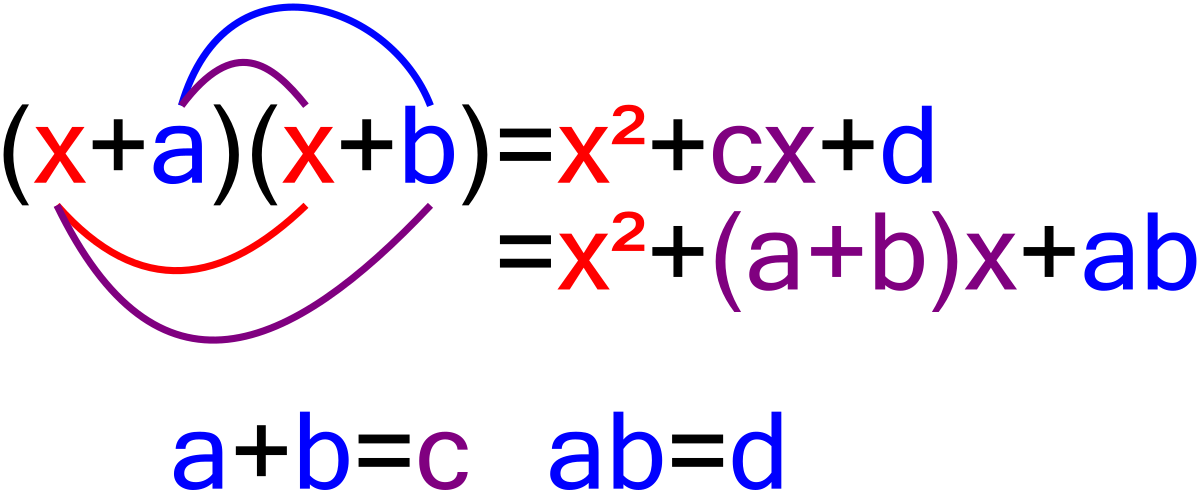 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 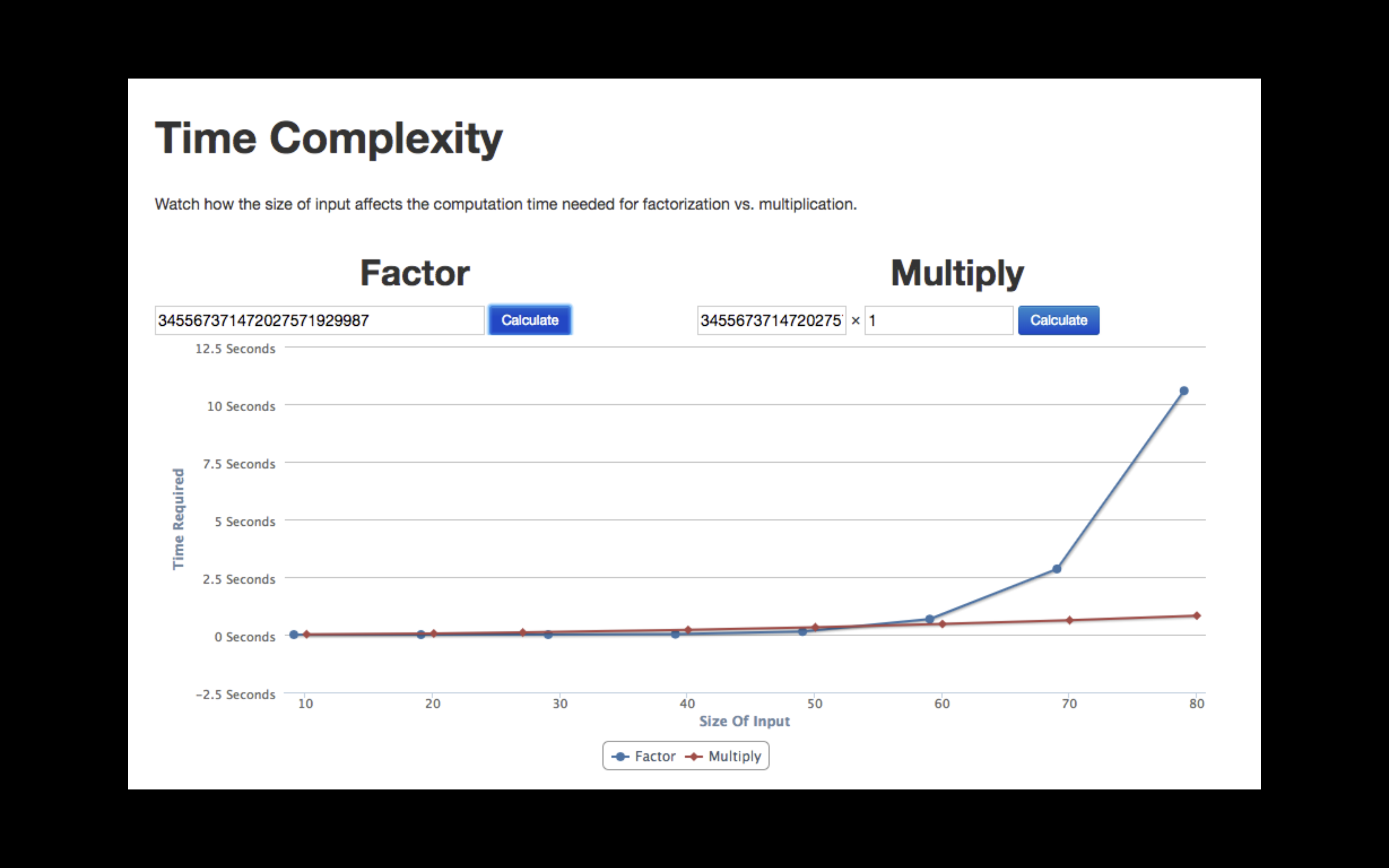 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | -2.png) Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 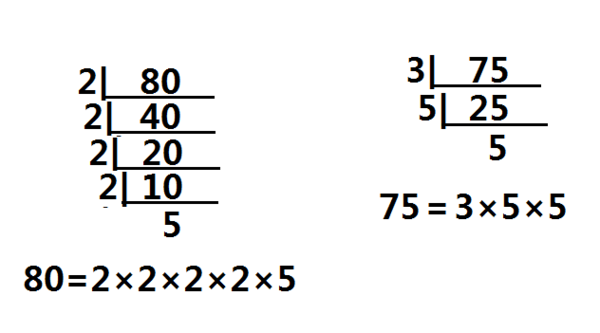 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 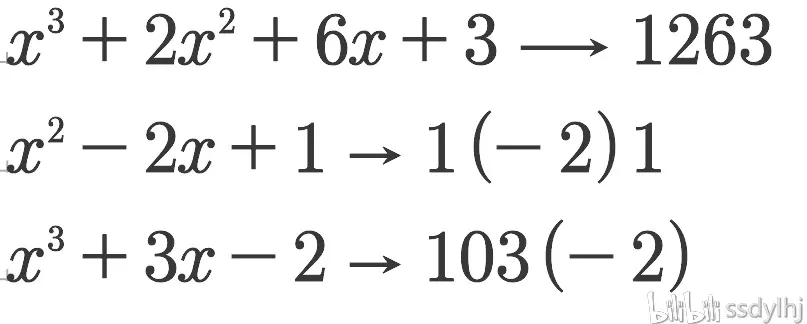 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
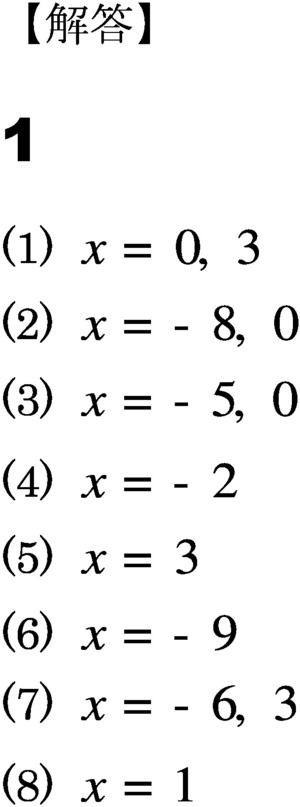 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 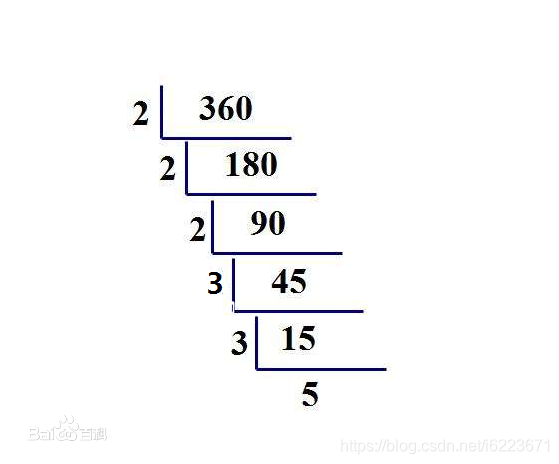 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
-4.png) Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 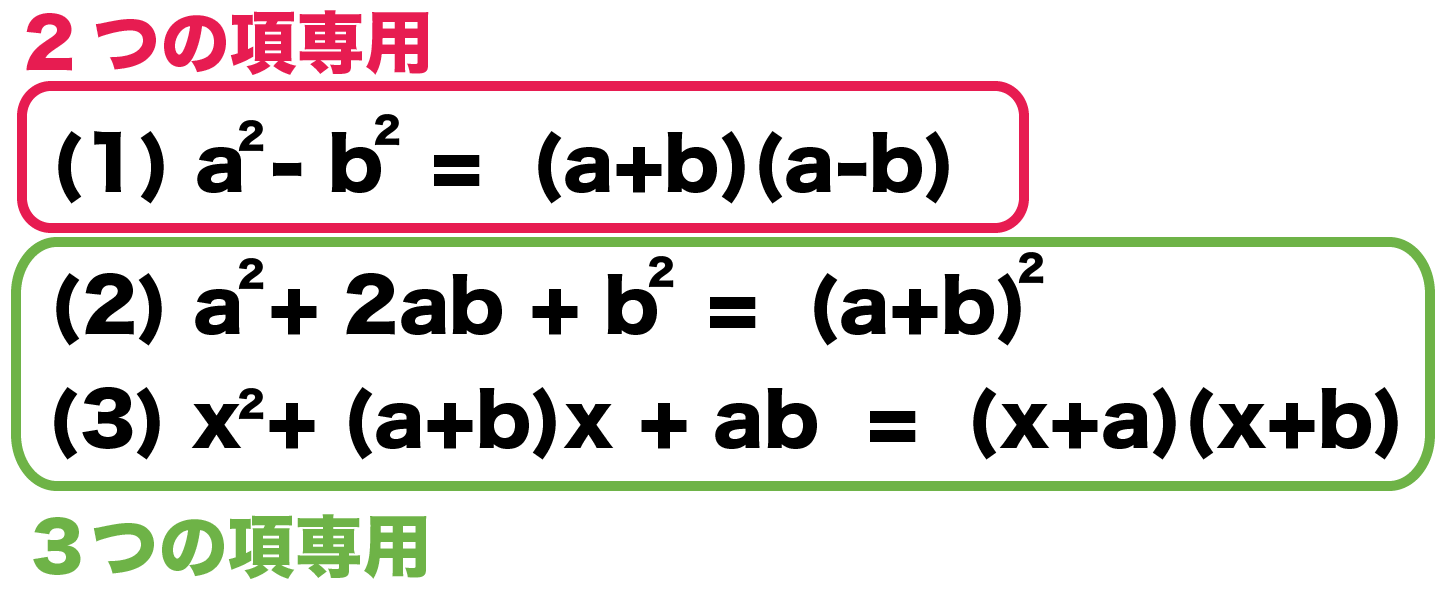 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | 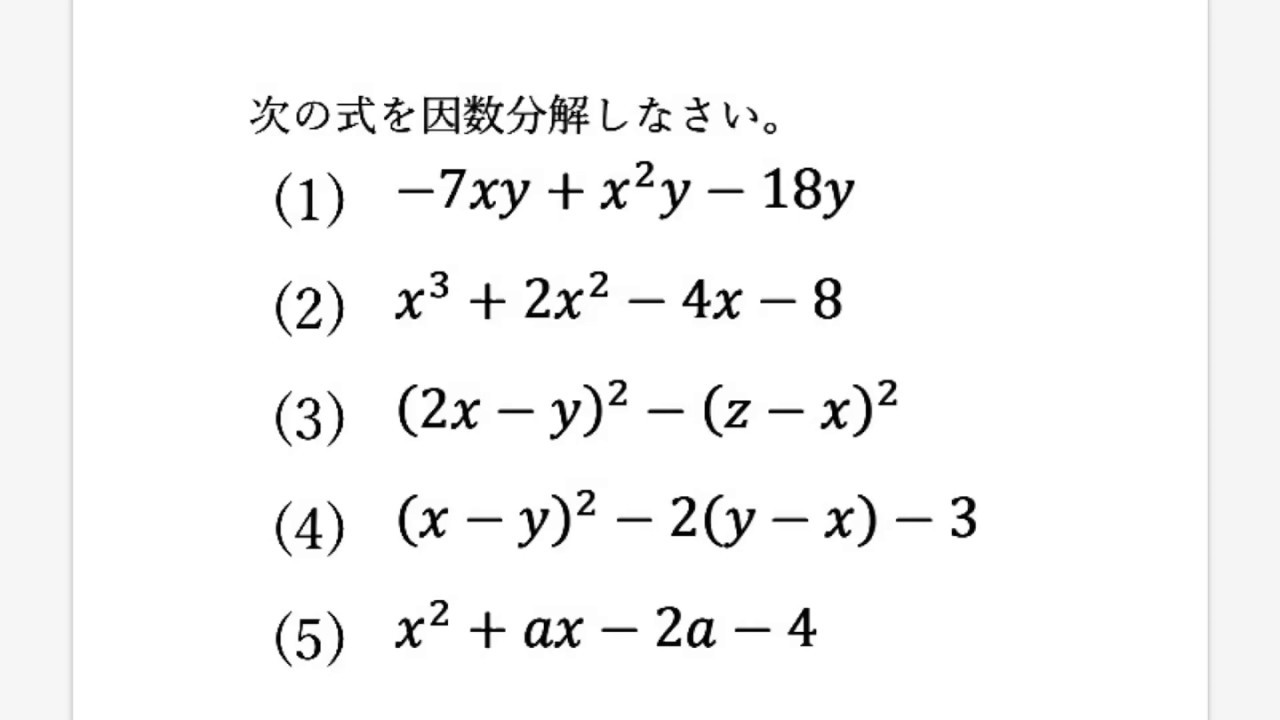 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
-3.png) Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna | Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
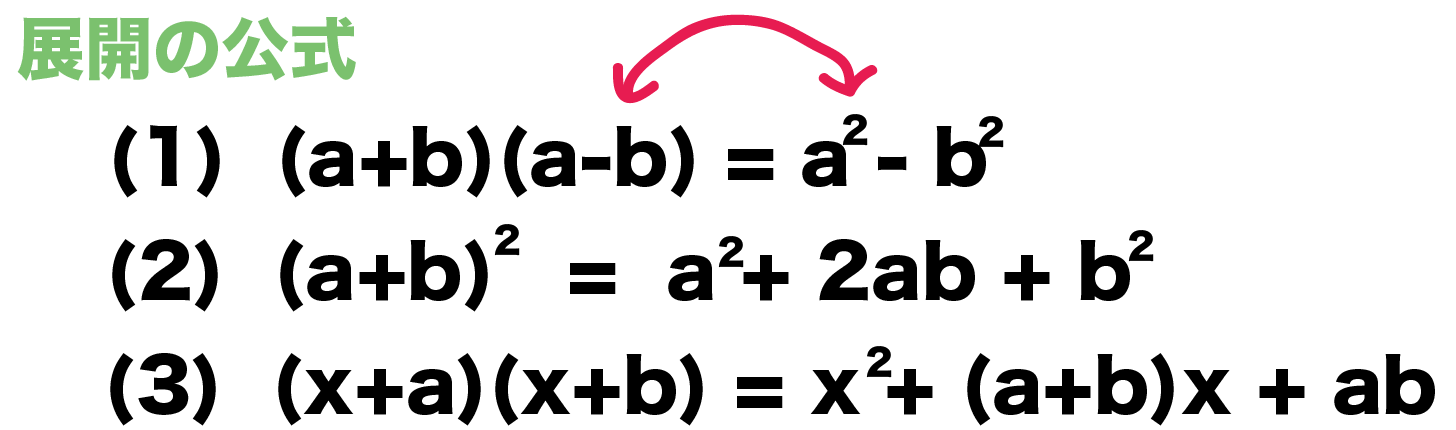 Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |  Pat甲级1059 Prime Factors 质因数分解 线性筛素数 Codeantenna |
今回は中3で学習する『因数分解』の単元から 共通因数でくくる というやり方について解説していきます。 共通因数でくくるというのは、因数分解の入門編みたいな感じですのでサクッと理解しちゃい 因数分解の公式2:x 2 (ab)xab=(xa)(xb) 次にこの公式について学習しましょう。 この公式のポイントはaとbが「 足すと左辺の真ん中の数に、掛けると左辺の一番右の数になる組み合わせを探す 」ことを判断するということです。
Incoming Term: 因数分解 中2 問題,
コメント
コメントを投稿